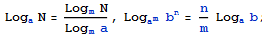-
常数函数
定义: y=C x∈（-∞,+∞)
应用: 如果y表示质点运动的速度，x表示时间，那么常数函数表示匀速直线运动，从时刻
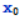到时刻
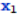的路程
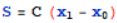就是图中阴影部分的面积. -
单项式函数
定义:
图像:
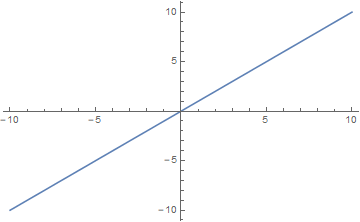
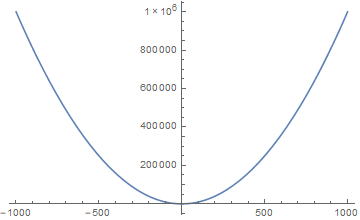
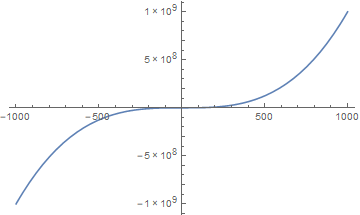
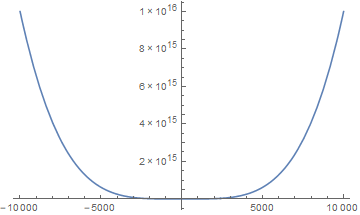
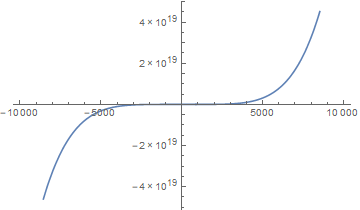
对于单项式函数，奇偶性恰与其次数的奇偶性相吻合
-
多项式函数
定义:
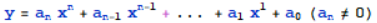
多项式函数中最高次数n称为多项式函数的次数。奇数次多项式至少有一个实根x0,使f(x0)=0
多项式函数有两个重要代数性质，两个多项式之和为多项式，两个多项式之积为多项式。具有加法、乘法两种运算的集合，构成一个环，它是交换代数研究的对象。
-
有理函数
定义:
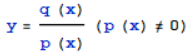
P(x),Q(x)都是多项式函数，通常我们假定P(x)和Q(x)没有非零次的公因式。由于零不能做分母，有理函数的定义域要在实数集中除去分母的零点。
-
幂函数
定义:
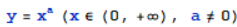
图像:
当a>0时，幂函数在(0,+∞)严格单调上升，当a>1时为凸函数，当0<a<1时为凹函数，当a<0时，幂函数(0,+∞)严格单调下降
-
指数函数
定义:
图像:
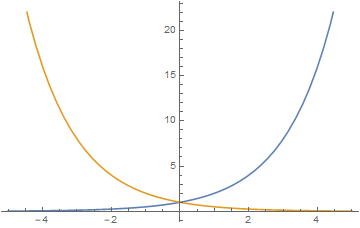
当a>1时，指数函数在(-∞,+∞)严格单调上升，当0<a<1时，指数函数在(-∞,+∞)严格单调下降
-
对数
定义:
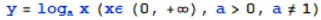
图像:
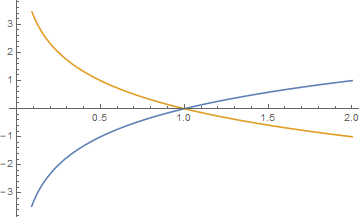
当a>1时，指数函数在(-∞,+∞)严格单调上升，当0<a<1时，指数函数在(-∞,+∞)严格单调下降
-
三角函数
定义:
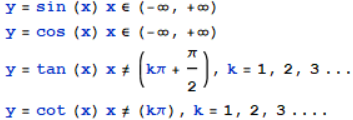
图像:
-
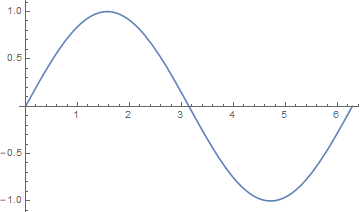
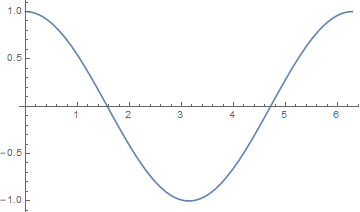
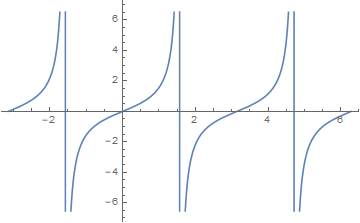
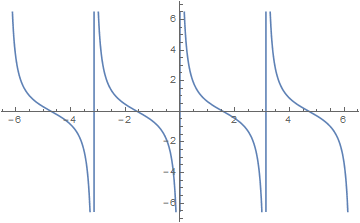
指数定律:
,
,
,
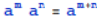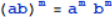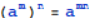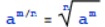如果a!=0,那么
,
,
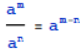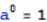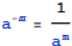
对数定理:
,
,
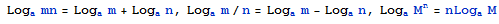